该文章是使用Gemini2.5来OCR生成的，原始笔记在这里

一、描述性统计

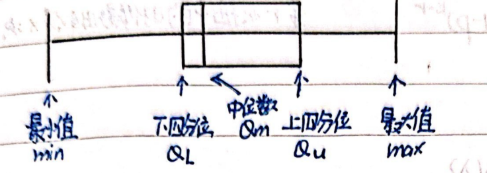
二、随机事件

1. 贝叶斯公式 (Bayes 公式) $P(A_K|B) = \frac{P(A_K B)}{P(B)}$

三、随机变量

1. 累计分布函数 $F(x) = P{X < x}$
2. 概率密度 $f(x) = F’(x)$
3. Binomial 分布 (二项分布) $X \sim B(n, p)$
   • a. $P{X=k} = C_n^k \cdot p^k \cdot (1-p)^{n-k}$
   • b. $E(X) = np$
   • c. $D(X) = np(1-p)$
4. Geometric 分布 (几何分布) $X \sim G_e(p)$
   • 描述：在一系列 Bernoulli 试验中，第一次成功所需的次数
   • a. $E(X) = \frac{1}{p}$
   • b. $D(X) = \frac{1-p}{p^2}$
   • c. (无记忆性) $P{X > m+n | X > m} = P{X > n}$
   • d. $P{X=k} = p(1-p)^{k-1}$
5. Hyper-geometric 分布 (超几何分布) $X \sim HypG(N, K, n)$
   • 描述：不放回抽取。总数 N，目标数 K，抽 n 个。X 为抽出几个目标。
   • a. $P(X=k) = \frac{C_K^k \cdot C_{N-K}^{n-k}}{C_N^n}$
   • b. $E(X) = n \cdot \frac{K}{N}$
   • c. $D(X) = [n \cdot \frac{K}{N}(1-\frac{K}{N})] \cdot \frac{N-n}{N-1}$
6. Pascal 分布 $X \sim Nb(r, p)$
   • 描述：第 r 次成功所需的次数
   • a. $P(X=k) = C_{k-1}^{r-1} \cdot p^r \cdot (1-p)^{k-r}$
   • b. $E(X) = \frac{r}{p}$
   • c. $D(X) = \frac{r(1-p)}{p^2}$
7. Poisson 分布 (泊松分布) $X \sim \pi(\lambda)$
   • 描述：平均每小时发生 $\lambda$ 次，一个小时发生 k 次的概率
   • a. $P(X=k) = \frac{\lambda^k}{k!} e^{-\lambda}$
   • b. $E(X) = \lambda$
   • c. $D(X) = \lambda$
8. 均匀分布 $X \sim U(a, b)$
   • a. $E(X) = \frac{a+b}{2}$
   • b. $D(X) = \frac{(b-a)^2}{12}$
   • c. $U(0, 1)$ 称为标准均匀分布
9. 指数分布 $X \sim Exp(a)$ 或 $X \sim E(a)$

   • a.

     $$ F(x) = \begin{cases} 1 - e^{-ax}, & x > 0 \\ 0, & x \le 0 \end{cases} $$

   • b. 可靠性函数 $R(t) = P{X > t} = 1 - F(t) = e^{-at}$

   • c. $f(x) = a e^{-ax}$

   • d. 无记忆性 $P{X > s+t | X > s} = P{X > t}$

   • e. $E(X) = \frac{1}{a}$

   • f. $D(X) = \frac{1}{a^2}$

10. 正态分布 $X \sim N(\mu, \sigma^2)$
    • a. $f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$
    • b. $\mu$ 为平均值，决定位置
    • c. $\sigma$ 为方差，$\sigma$ 越大，图形越矮越宽 (笔记原文如此，但 $\sigma$ 通常指标准差)
    • d. $E(X) = \mu$
    • e. $D(X) = \sigma^2$
    • f. 标准正态 $N(0, 1)$，其 $f(x)$ 为 $\phi(x)$，$F(x)$ 为 $\Phi(x)$
    • g. $F(x) = \Phi(\frac{x-\mu}{\sigma})$
    • h. $f(x) = \frac{1}{\sigma} \phi(\frac{x-\mu}{\sigma})$
11. $D(X) = E{(X-E(X))^2}$
    • $D(X)$ 也写作 $\text{Var}(X)$
12. 标准差/均方差 $\sigma_X = \sigma(X) \triangleq \sqrt{D(X)}$
13. $D(X) = E(X^2) - E^2(X)$
14. Chebyshev 不等式 $P{|X-\mu| \ge k} \le \frac{\sigma^2}{k^2}$

四、多维随机变量

1. 联合分布函数 $F(x, y)$
2. 边缘分布函数 $F_X(x) = F(x, +\infty)$
3. 联合密度函数 $f(x, y)$
4. 边缘密度函数 $f_X(x) = \int_{-\infty}^{+\infty} f(x, y) dy$
5. 独立性: 有 $F(x, y) = F_X(x) \cdot F_Y(y)$ (离散型) 或 $f(x, y) = f_X(x) \cdot f_Y(y)$ (连续型)
6. 条件分布列 $P_{i|j} = P{X=x_i | Y=y_j} = \frac{p_{ij}}{p_{\cdot j}}$
7. 条件密度函数 $f(x|y) = \frac{f(x, y)}{f_Y(y)}$
8. 条件分布函数 $F_{X|Y}(x|y) = \int_{-\infty}^{x} f_{X|Y}(t|y) dt$
9. 数学期望
   • (离散) $E(g(X, Y)) = \sum_i \sum_j g(x_i, y_j) \cdot P{X=x_i, Y=y_j}$
   • (连续) $E(g(X, Y)) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} g(x, y) \cdot f(x, y) dx dy$
10. $E(\sum_{k=1}^{n} X_k) = \sum_{k=1}^{n} E(X_k)$
11. 当 $X_i$ 相互独立时：
    • $D(\sum_{k=1}^{n} X_k) = \sum_{k=1}^{n} D(X_k)$
    • $E(\prod_{i=1}^{n} X_i) = \prod_{i=1}^{n} E(X_i)$
12. 柯西-许瓦兹不等式 $|E(XY)|^2 \le E(X^2)E(Y^2)$
13. $D(X+Y) = D(X) + D(Y) + 2E((X-\bar{X})(Y-\bar{Y}))$
14. 协方差 $\text{Cov}(X, Y) = E{(X-\bar{X})(Y-\bar{Y})} = E(XY) - E(X)E(Y)$
15. $\text{Cov}(X_1+X_2, Y) = \text{Cov}(X_1, Y) + \text{Cov}(X_2, Y)$
16. 相关系数 $\rho_{XY} = \frac{\text{Cov}(X, Y)}{\sqrt{D(X)}\sqrt{D(Y)}}$